Question 61
(Multiple Choice)
Use the following information to answer the questions below.
Unicellular yeasts can be represented as spheres,whereas filamentous hyphae more closely resemble cylinders.As these two geometric figures increase in size,their surface area-to-volume ratios change.The following tables demonstrate how this ratio changes,first for spheres,and second for cylinders.For the cylinder,girth (i.e.,radius,r)will remain constant,whereas length,L,will increase.Note the formulas below the respective tables.
A sphere's change in surface area and volume with increasing radius,r

Area of a Sphere = 4r² Volume of a Sphere = 4/3r³
A cylinder's change in surface area and volume with increasing length,L
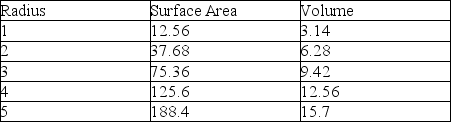
Area of a Cylinder = 2(r²)+ 2rL Volume of a Cylinder = r²ᴸ
-Which statement is a correct interpretation of the data in the previous tables?
A)As a sphere gets bigger, its surface area and volume increase at about the same pace.
B)As a cylinder gets bigger, its surface area increases at a greater pace than does its volume.
C)As a cylinder gets bigger, its volume increases at about the same pace at which the volume of a sphere increases.
D)As spheres and cylinders get bigger, the surface area of a cylinder increases at a faster pace than does the surface area of a sphere.
Answer